По сравнению с изотермической кинетической мо­делью модель реактора и реакционного узла каталитического риформинга требует только дополнительного проведения теплового расчета процесса в реакторе. Задача облегчается тем, что промышленные реакторы риформинга в хорошем приближении можно рассматривать как адиабатические. Тогда система уравнений (8.2)—(8.6) допол­няется уравнением теплового баланса

с начальными условиями для первого реактора

и для последующих:

где G — массовый поток газосырьевой смеси; с_р — усредненная теплоемкость газо­сырьевой смеси; Т — температура по координате реактора; q_ui —усредненная тепло­та u-й реакции для i-ro класса углеводородов; Т_п — температура потока из печи промежуточного подогрева.

Практика, однако, показала, что в плане надежности и простоты вычислительной процедуры уравнение (8.7) следует заменить  рекурентным уравнением (8.10).  При  этом поскольку интервал рабочей температуры реактора относительно невелик, зависимостью тепло­емкости от температуры можно пренебречь:

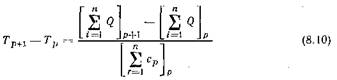
Здесь ∑ Q — суммы молярных теплот образования компонентов реакционной смеси; р — номер шага интегрирования; с_р — молярные теплоемкости компонентов реакционной смеси.

Имея математическую модель реактора в виде системы уравнений (8.2)—(8.6) и (8.10) можно провести оптимизационные расчеты реак­ционного узла риформинга в отношении числа реакторов в узле, рас­пределения катализатора и профиля температур в них. Методики такого рода расчетов изложены, например, в монографиях [323] и [314]. Расчеты, проведенные в работах [313] и [315] показали, что процесс мало чувствителен к распределению катализатора по реакторам, поскольку вносимые при этом изменения можно компенсировать за счет входных температур реакторов.