Термодинамика восстановления нитробензола в анилин в газовой фазе
Восстановление нитробензола в анилин в газовой фазе протекает по уравнению:(16)
![]()
Тепловой эффект этой реакции можно рассчитать, пользуясь имеющимися в литературе значениями теплоты образования веществ в стандартных условиях [16, 17] и приведенными в табл. 12.
Таблица 11. Зависимость температуры ВНС на выходе из испарителя от температуры нитробензола (t1) и водорода (t2) при т = 15
t 2 | Температура ВНС, "С | |||||||
t1=60°С | t1=80°С | t1=100 °С | t1=120 °С | t1=140°С | t1=160 °С | t1=180 °С | t1=200 °С | |
180 | 77, 6 | 83, 2 | 88, 9 | 94, 7 | 100, 4 | 106, 1 | 111, 9 | 117, 6 |
200 | 91, 8 | 97, 5 | 103, 2 | 109, 0 | 114, 7 | 120, 4 | 126, 2 | 131, 9 |
220 | 106, 1 | 111, 8 | 117, 5 | 123, 3 | 129, 0 | 134, 7 | 140, 4 | 146, 2 |
240 | 120, 4 | 126, 1 | 131, 8 | 137, 6 | 143, 3 | 149, 0 | 154, 7 | 160, 5 |
260 | 134, 7 | 140, 4 | 146, 1 | 151, 9 | 157, 6 | 163, 3 | 169, 0 | 174, 8 |
Таблица 12. Теплота образования (из элементов в стандартных условиях) и теплота испарения веществ, участвующих в реакции восстановления нитробензола
Вещество | Теплота образования H298 кДж/моль | Теплота испарения Ни кДж/моль | Вещество | Теплота образования H298 , кДж/моль | Теплота испарения Ни кДж/моль |
Нитробензол (ж) | 15, 91 | 40, 74 | Анилин (ж) | 31, 11 | 44, 34 |
Водород (г) | 0 | — | Вода (ж) | —286, 03 | 44, 05 |
Общий тепловой эффект реакции в стандартных условиях равен:
H298 = 31, 11 — 286, 03 • 2 — 15, 91+ 44, 34+ 44, 05 • 2 — 40, 74 = -465, 16 кДж/моль (17)
Имеющаяся в литературе экспериментальная зависимость теплового эффекта восстановления от температуры [102] дает завышенные результаты, однако, зная зависимость теплоемкости реагентов от температуры, нетрудно вычислить тепловой эффект с точностью, достаточной для инженерных расчетов. Зависимость теплоемкости от температуры (Т. К) представлена в виде полинома:
![]() (18)
(18)
Коэффициенты ai, bi и с, для веществ, участвующих в реакции, равны:
Вещество | а;. Дж/(моль-К) | b;. 103, Д&/(моль. К2) | Cj-106. Дж/(моль. К3) |
Нитробензол (г) | 28, 85 | 318, 00 | —94, 96 |
Водород (г) | 29, 10 | —0, 84 | 2, 01 |
Анилин (г) | 7, 75 | 369, 11 | —128, 99 |
Вода (г) | 30, 14 | 11, 30 | — |
По этим данным можно рассчитать вклад каждого слагаемого в зависимость теплового эффекта от температуры:
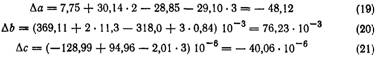
На основании уравнения Кирхгофа нетрудно установить зависимость теплового эффекта от температуры:
![]() (22)
(22)
Подставляя значения коэффициентов из (17) и (19)—(21) в уравнение (22) при Т == 289,2 К, получим Hr= 453,87 кДж/моль. Тогда окончательная зависимость будет иметь вид:
![]() (23)
(23)
Тепловой эффект при различных температурах приведен в табл. 13.
Для всех веществ, участвующих в реакции, известно изменение энергии Гиббса [22]; его суммарное изменение в реакции равно:
![]() (24)
(24)
Логарифм константы равновесия можно определить из уравнения:
![]() (25)
(25)
Из уравнения Вант-Гоффа можно определить зависимость константы равновесия от температуры (1 — константа интегрирования):
![]() (26)
(26)
Подставляя в уравнение (26) значения К при 298, 2 К из (25), Hr98 из (17) и значения Да, Àb и Ас из (19)—(21), получим константу интегрирования. Окончательная зависимость константы равновесия от температуры будет иметь вид:
lgK = 8,91+ 24280/T — 5,783lgT + 1,99•10-3T - 0,349•10-6T2 (27)
Константы равновесия при разных температурах тоже приведены в табл. 13.
Приведенные расчеты показывают, что равновесие реакции восстановления нитробензола сильно сдвинуто в сторону анилина.
Таблица 13 Зависимость теплового эффекта и константы равновесия реакции восстановления нитробензола от температуры
Т, К | —Hr, кДж/моль | lgK | Т, К | —Hr, кДж/моль | lgK |
298 | 465, 16 | 76, 6 | 600 | 471, 89 | 34, 4 |
300 | 265, 24 | 76, 1 | 700 | 473, 44 | 28, 4 |
400 | 467, 87 | 55, 3 | 800 | 474, 78 | 23, 8 |
500 | 470, 05 | 42, 8 | 900 | 476, 04 | 20, 3 |
Зная константу равновесия, можно рассчитать равновесный состав газовой смеси по уравнению:
![]() (28)
(28)
где na,nH2O, nнб, nH2 — соответственно число молей анилина, воды, нитробензола и водорода в равновесной смеси; SN — общее число молей компонентов в равновесной смеси, Р—внешнее давление, МПа; дn—изменение числа молей реагирующих веществ в ходе реакции.
Если в реакцию вступает смесь нитробензола и водорода, в которой мольное соотношение реагентов равно 1: 10, то в равновесной смеси будет содержаться Х моль анилина, 2Х моль воды, (1—X) моль нитробензола и (10—ЗХ) моль воды; всего (11 — X} моль:
![]() (29)
(29)
Подставив в уравнение (29) значение К., например при 600 К (327°С), получим, что концентрация нитробензола в равновесной смеси составляет менее 10-12 мольной доли.